Tässä dokumentissa esittelen jonkin verran permutaatioryhmiksi kutsuttujen matemaattisten objektien teoriaa. Koska tavoitteena on soveltaa teoriaa Rubikin kuution tutkimiseen (ratkaisualgoritmi, tilojen lukumäärän laskeminen), en pyri läheskään kattavaan esitykseen tästä laajasta alueesta. Esitys on varsin tiivis, mutta (etenkin päivitysten jälkeen) toivottavasti sellainen, jota matemaattisesti lahjakas lukiolainen pystyy helposti seuraamaan. Kaikki todistukset ovat helposti löydettävissä Turun yliopiston kahden ensimmäisen vuoden matematiikan kurssien Algebran peruskurssi ja Algebra luentomonisteista. Osan perusteluista olen ottanut mukaan päätekstiin ja osan kerännyt linkkien taakse.
Tarkoitukseni ei ole esittää tai etsiä mahdollisimman nopeaa Rubikin kuution ratkaisumenetelmää. Esitän ainoastaan erään algebrallisen tavan lähestyä tätä pulmaa. Esitetty menetelmä on matematiikalle tyypillinen "Divide and conquer"-algoritmi, joka on valittu nimen omaan algebrallisen luonteensa vuoksi.
Kiitokseni Taneli Huuskoselle ja Valtteri Niemelle. Heidän kanssaan käymäni keskustelut ovat kristalloineet tässä esitettäviä ajatuksia.
Olkoon X jokin äärellinen joukko. Bijektiivistä funktiota f, jolle X on sekä lähtö- että
maalijoukko sanotaan joukon X permutaatioksi. Vaaditaan siis, että
jokainen joukon X alkio esiintyy tarkalleen yhden alkion kuvana. Funktioita
kuvataan usein diagrammeina, joissa nuolet liittävät lähtöjoukon alkiot
kuviinsa. Koska permutaation tapauksessa lähtö- ja maalijoukot yhtyvät,
on luonnollisempaa piirtää joukko X vain kerran, jolloin jokaisesta
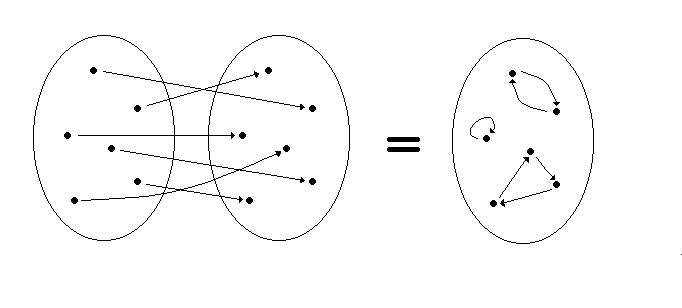
alkiosta lähtee ja saapuu tarkalleen yksi nuoli. Ohessa kuva 6 alkion
joukon permutaatiosta.

Kuvan oikeanpuoleisesta osasta huomataan, että permutaatiota kuvaavat nuolet muodostavat sulkeutuvia ketjuja. Tällaisia ketjuja kutsutaan sykleiksi. Jos syklissä on n kappaletta nuolia (tai alkioita), sanotaan sitä lyhyesti n-sykliksi.
Ylläolevan tapaiset diagrammit vievät paljon tilaa. Kompaktimpaan esitykseen
pääsemiseksi nimetään (numeroidaan) joukon X alkiot luvuilla 1,2, jne.
Tällöin funktio f voidaan kuvata lyhyesti vektorina, jossa luetellaan kuvat
f(1), f(2), jne. Algebrassa käytetään yleensä
vektorimerkinnän asemasta syklimerkintää, jossa
sulkuihin kirjoitetaan peräkkäin sykliin kuuluvat alkiot nuolten kulkusuunnan
määräämässä järjestyksessä. Permutaatiota vastaa tällöin sulkulauseke,
jossa sulkujen lukumäärä on sama kuin ko. permutaation syklien lukumäärä.
Huomaa, että tällainen sykliesitys ei ole tarkkaan ottaen yksikäsitteinen,
sillä syklien aloituskohdat voidaan valita vapaasti. Esimerkiksi 3-syklit
(123) ja (231) molemmat tarkoittavat permutaatiota, jossa ykkönen kuvautuu
kakkoseksi, joka puolestaan kuvautuu kolmoseksi, joka lopulta kuvautuu
takaisin ykköseksi. Alla on esitetty äskeisen 6 alkion joukon permutaatio
vektori- ja syklimerkintää käyttäen. Yleensä tehdään sopimus, ettei
1-syklejä merkitä lainkaan näkyviin. Poikkeuksen tälle muodostaa
pelkästään 1-sykleistä koostuva ns. identiteettipermutaatio, jolle
jätetään näkyviin yksi 1-sykli, esimerkiksi (1).
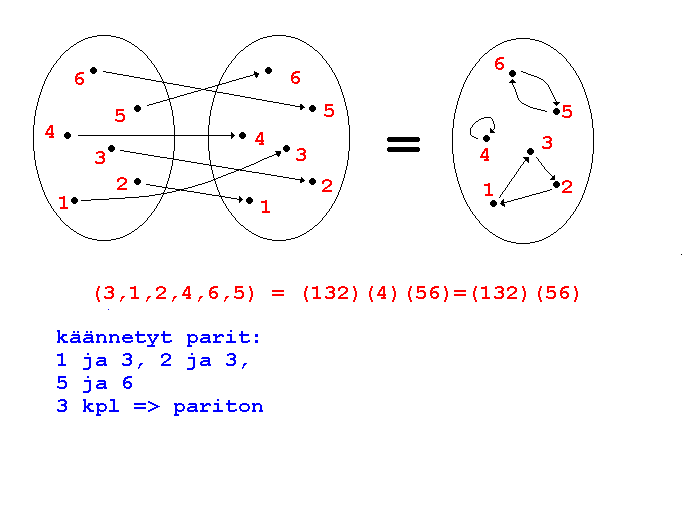
Kun tarkastellaan permutaation vektoriesitystä, huomataan että siinä jotkin lukuparit ovat "väärässä järjestyksessä" eli isompi luku esiintyy vektorissa ensin. Esimerkkipermutaatiossamme tällaisia käännettyjä pareja on kolme kappaletta. Käännettyjen parien lukumäärä sinänsä ei ole kovin mielenkiintoinen käsite, sillä se riippuu alkioiden numeroimisjärjestyksestä. Numerothan esiintyvät tarkastelussa vain joukon X alkioiden "nimilappuina". (Esimerkkinä voit todeta, että jos yo. kuvassa vaihdetaan alkioiden 1 ja 5 nimilaput keskenään, niin käännettyjen parien määrä nousee kolmesta kolmeentoista.) Tärkeää on, että käännettyjen parien pariteetti (parillinen vai pariton) on numerointijärjestyksestä riippumaton. Tämä seikka todistetaan mm. Turun yliopiston Algebran peruskurssilla. Permutaatiota sanotaankin parilliseksi tai parittomaksi riippuen siitä, onko sen käännettyjen parien lukumäärä parillinen vai pariton luku. Yllä mainitun tuloksen nojalla permutaation pariteetti on hyvin määritelty käsite, eli ei riipu käytetystä alkioiden numerointitavasta. Lukija voi harjoitustehtävänä todeta, että n-sykli (tai pikemminkin permutaatio, jossa on yksi n-sykli ja jossa loput alkiot pysyvät paikallaan, eli kuuluvat 1-sykliin) on parillinen, jos n on pariton ja päinvastoin.
Tunnetusti bijektion käänteiskuvaus on niin ikään bijektio. Samoin kahdesta joukon X bijektiosta voidaan muodostaa kolmas annettujen bijektioiden kuvaustulona eli kompositiona. Käytetään joukon X kaikkien permutaatioiden joukosta merkintää S(X). Olkoon G joukon S(X) epätyhjä osajoukko. Joukolla G voi olla sellainen ominaisuus, että sen alkioiden kompositiot kuuluvat myös joukkoon G. Tällöin sanotaan, että G on permutaatioryhmä. Jos G on permutaatioryhmä, niin sen alkioiden käänteiskuvaukset myös kuuluvat joukkoon G. Todistus.
Nähdään, että esimerkiksi koko S(X) on permutaatioryhmä. Jos X on lukujen 1,2,3,...,n muodostama joukko, käytetään lyhennysmerkintää Sn. Koska n alkiota voidaan kirjoittaa n! eri järjestyksessä, tämän ryhmän alkioiden määrä on n!. Permutaatioiden kertolasku on näin tavallista funktioiden yhdistämistä. Koska yleensä funktioiden kompositiomerkinnässä (esimerkiksi f o g) viimeksi kirjoitettua funktiota sovelletaan ensin, on muistettava, että permutaatioidenkin tuloa on luettava "oikealta vasemmalle". Siis esimerkiksi ryhmässä S4
Voidaan ajatella parilliset permutaatiot plusmerkkisiksi ja parittomat
miinusmerkkisiksi. Tällöin voidaan helpohkosti (TY, Algebran peruskurssi)
todistaa seuraava luonnollisen tunteinen tulos.
Tulosäännöstä nähdään heti, että joukon X parilliset permutaatiot muodostavat permutaatioryhmän Alt(X), niin sanotun alternoivan ryhmän. Jos X on joukko 1,2,...,n, käytetään merkintää An. Lukijalle harjoitustehtäväksi jätetään sen osoittaminen, että kaikista permutaatioista tasan puolet on parillisia ja toinen puoli parittomia. Ryhmässä An on siis n!/2 alkiota.
Yllä jo näimme, miten parillinen permutaatio (12)(34) voitiin esittää 3-syklien tulona. Voidaan osoittaa, että itse asiassa jokainen parillinen permutaatio voidaan esittää 3-syklien tulona. Todistus.
Yksi keskeinen permutaatioryhmiä koskeva keskeinen seikka on, että ryhmä Alt(X) on ns. yksinkertainen ryhmä, jos joukossa X on ainakin 5 alkiota. Rubikin kuutiota ratkottaessa ei tällä muutoin tärkeällä tuloksella ole merkitystä. Tästä kuitenkin viime kädessä johtuu, ettei viidettä ja sitä korkeampaa astetta oleville yhtälöille voida johtaa algebrallista ratkaisukaavaa. Lisätietoja näistä aiheista saat osallistumalla algebran kurssille.
Konjugointi
Jos s ja t ovat joukon X permutaatioita, niin permutaation
s t s-1 sanotaan muodostetun konjugoimalla permutaatiota
t permutaatiolla s. Meidän kannaltamme tärkeää on havaita, että
konjugointi säilyttää syklirakenteen, toisin sanoen permutaatiossa t
ja sen konjugaateissa esiintyvät yhtä pitkät syklit: konjugoitu permutaatio
s t s-1
operoi alkioihin kuten alkuperäinenkin permutaatio t, mutta konjugoiva
permutaatio s on ensin vaihtanut alkioiden "nimilappuja/numerointia".
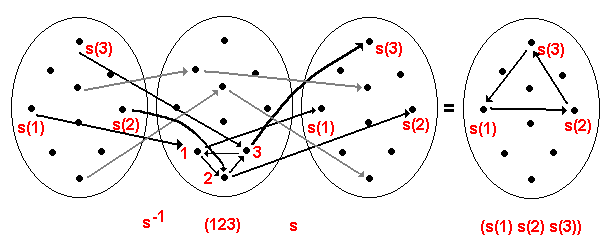
Oheinen kuva valaisee tätä seikkaa 3-syklin tapauksessa. Kuvassa
s ja sen käänteiskuvaus on kuvattu normaalina nuolikuviona, jossa
lähtö ja maalijoukko on erotettu. Konjugoitava 3-sykli t sen sijaan
on kuvattu syklinä joukon X vasemmalta lukien toisessa kopiossa.
1-syklit on jätetty merkitsemättä.
Kuvan harmaat nuolet esittävät "mielivaltaisten" 3-syklin ulkopuolisten
alkioiden kuvautumista.
Sanomme, että permutaatiot s ja t kommutoivat, jos niiden kuvaustulo ei riipu tekijöiden järjestyksestä, eli st = ts. Aiemmin näimme, että 3-syklit (123) ja (124) eivät kommutoi, koska (123)(124)=(13)(24) ja (124)(123)=(14)(23). Tyypillinen tilanne (ei kuitenkaan ainoa), jolloin s ja t kommutoivat, on sellainen, missä s ja t liikuttavat eri alkioita. Tällöin joukko X voidaan jakaa kahtia osiin A ja B siten, että s pitää kaikki osan B alkiot paikallaan ja t pitää kaikki osan A alkiot paikallaan. Esimerkiksi ryhmässä S5 permutaatiot s=(123) ja t=(45) kommutoivat:
Jos permutaatiot s ja t eivät kommutoi, niin epäkommutatiivisuuden määrää voidaan "mitata" laskemalla niiden kommutaattori [s,t]=sts-1t-1. Helposti nimittäin nähdään, että [s,t] on identiteetti kuvaus, tarkalleen silloin kun s ja t kommutoivat.
Millaisia kommutaattoreita tarvitsemme? Muutetaan äskeistä kommutoivaa tilannetta minimaalisesti siten, että t pitää osan A alkiot paikallaan ainoastaan yhtä (sanokaamme x) lukuun ottamatta. Oletetaan lisäksi, että s ei pidä alkiota x paikallaan. Tilanne on siis oheisen kuvan mukainen. Kuvan harmaa katkoviiva erottaa osat A ja B toisistaan.
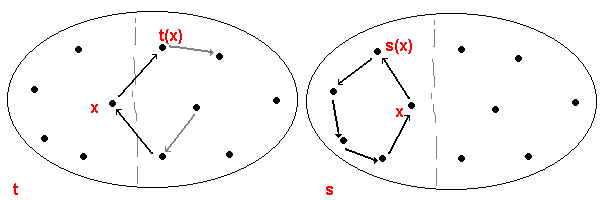
Osoittautuu, että tällöin kommutaattori [s,t] on 3-sykli (x s(x) t(x)). Seuraavassa taulukossa on laskettu, miten kommutaattori kuvaa näitä kolmea alkiota - kullakin vaakarivillä on rivin ensimmäisenä mainitun alkion kuvautuminen kommuttaattorin neljässä vaiheessa:
| t-1 | s-1 | t | s | |
|---|---|---|---|---|
| x | t-1(x) | t-1(x) | x | s(x) |
| s(x) | s(x) | x | t(x) | t(x) |
| t(x) | x | s-1(x) | s-1(x) | x |
Tämä tulee jatkossa olemaan tärkeä tapa tuottaa 3-syklejä.
Rubikin kuutio on 80-luvun alussa markkinoille tullut
unkarilaisen insinöörin Ernö Rubikin kehittämä kohtuullisen vaativa pulmapeli.
Siinä on kuutio jaettu joka suuntaan kolmeen eri kerrokseen, joita kutakin
voidaan kiertää muista riippumattomasti. Näin kuution kaikki kuusi sivua
jakautuvat yhdeksäksi ruuduksi, jotka alkutilanteessa ovat kaikki
samanvärisiä. Alla on kuva tällaisesta sekoittamattomasta kuutiosta. Kuvan
vasemmassa osassa on esitetty kolme etualalla olevaa kuution sivua ja
oikealla kolme taustalla olevaa sivua ikään kuin etualan sivut olisi
poistettu. Tässä kuutiossa vastakkaisten sivuparien värit ovat siis
punainen ja musta, valkoinen ja keltainen, sininen ja vihreä. Myynnissä
olleissa kuutioissa esiintyi muitakin väriyhdistelmiä. Itse värit eivät
ratkaisualgoritmin kannalta tietenkään ole olennaisia - ainoastaan
eriväristen sivujen suhde toisiinsa (mitkä värit ovat vastakkaisilla
sivuilla, mitkä kolme yhtyvät jossakin kuution kärjessä jossakin
tietyssä järjestyksessä jne).
Alkutilanne: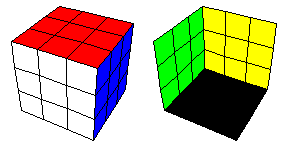
Kuution erisuuntaisia kerroksia kiertämällä tuon yksivärisen alkutilanteen saa sekoitettua varsin nopeasti tunnistamattomaksi värien sekamelskaksi. Pulmapelin ideana on palauttaa sekoitettu kuutio yllä kuvattuun alkutilaan. Koska kuution osat voivat olla toisiinsa nähden yli 43 triljoonassa eri asennossa, on selvää, että satunnaisella kuution kääntelyllä onnistumismahdollisuudet ovat häviävän pienet.
Kuvassamme kuutio on asennossa, jossa edessä on valkoinen sivu, ylhäällä punainen ja oikealla sininen. Mitään olellista ei tapahdu, jos käännämme koko kuution sellaiseen asentoon, jossa edessä on punainen sivu, ylhäällä keltainen (alkuperäinen takasivu) ja oikealla sininen. Matemaattiselle kielenkäytölle tyypillisen tapaan kutsumme kahta tällaista kuution tilaa, jotka saadaan toisistaan koko kuutiota kääntämällä ekvivalenteiksi . Tällöin siis kuution osien keskinäinen asento ei muutu, ainoastaan katselemme kuutiota eri suunnasta. Jos emme pidä kuution ekvivalentteja tiloja eri tiloina, voimme olettaa, että sivujen keskellä olevat ruudut pysyvät koko ajan paikallaan ja tavallaan näin määräävät koko sivun värin (pyrkimyksenähän on yksivärinen sivu). Jos olet joskus purkanut Rubikin kuution osiinsa, vakuuttunet helposti siitä, etteivät nämä keskiruudut itse asiassa koskaan liiku! Tarkoituksenmukaisuussyistä alla kuvattujen siirtosarjojen aikana joskus keskiruutujenkin värit vaihtuvat, mutta tähän olen turvautunut ainoastaan siksi, että kulloinkin "oleelliset" tapahtumat olisivat etualalla.
Kuution erisuuntaisia kerroksia voidaan kutakin kääntää neljänneskierros kahteen eri suuntaan. Jatkoa varten olen nimennyt tietyt tällaiset siirrot kuvaavilla nimillä: etumyota, etuvasta, oikeaalas, oikeaylos, keskialas, keskiylos, vasenalas, vasenylos, kansiplus, kansimiinus, valiplus, valimiinus, pohjaplus, pohjamiinus. Ohessa kuvia näistä siirroista:
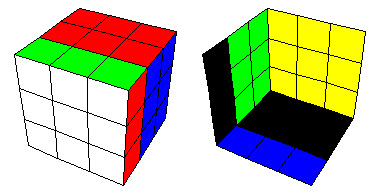
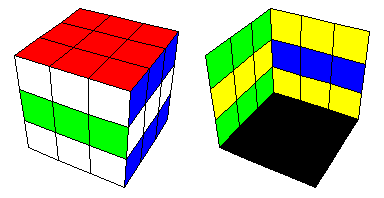
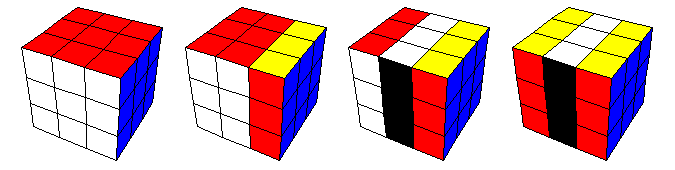
Käytän jatkossa siirtosarjoista merkintää, jossa lainausmerkkien sisällä on pilkuilla erotettuna yllä mainittuja perussiirtoja. Tässä yhteydessä (päinvastion kuin permutaatioista puhuttaessa) on luonnollista lukea siirtosarjaa vasemmalta oikealle.
Yllä kuvattu ekvivalenssi tarkoittaa nyt esimerkiksi sitä, että alkutilanteeseen voimme yhden siirron siirtosarjan "keskiylos" asemesta tehdä siirtosarjan "vasenalas,oikeaalas" - näiden siirtosarjojen vaikutus kuution osien keskinäisiin suhteisiin on sama. Käännä mielessäsi siirtosarjan "keskiylos" jälkeen koko kuutiota neljänneskierros siten, että yläsivu tulee etusivuksi - kuutio näyttää tarkalleen samalta kuin siirtosarjan "vasenalas,oikeaalas" jälkeen. Näin voimme teoriassa luopua sivujen keskiruutuja liikuttavista perussiirroista. Usein saadaan kuitenkin selkeämpi kuva siirtosarjasta, jos siihen ei tarvitse sisällyttää koko kuution kääntämistä = katselukulman vaihtoa.
Rubikin kuution permutaatioryhmät
Kuutiossa on useita erityyppisiä osia: 54 ruutua (9 kullakin sivulla), 6 sivun keskiruutua (1 kullakin sivulla), 8 kärkipalaa (pala, josta on näkyvissä 3 eriväristä ruutua) ja 12 särmäpalaa (pala, josta on näkyvissä 2 eriväristä ruutua). Perussiirrot permutoivat nyt sitten kutakin tyyppiä olevia osia (ruutuja, kärkiä ja särmiä). Selvästikään särmä- ja kärkipalat eivät koskaan voi sekoittua keskenään, eli kärkipala ei koskaan siirry särmäpalan paikalle tai päinvastoin. Rajoituksetta voimme olettaa tekevämme kuutioon vain keskiruudut paikallaan pitäviä perussiirtoja etumyota, etuvasta, takamyota, takavasta, oikeaalas, oikeaylos, vasenalas, vasenylos, kansiplus, kansimiinus, pohjaplus ja pohjamiinus - muut perussiirrothan saatiin näitä kombinoimalla ja katselukulmaa vaihtamalla.
Sanomme kunkin sivun keskiruudun värin määräävän kyseisen sivun värin. Edelleen sanomme kärki- tai särmäpalan olevan oikeassa paikassa, jos se on ruutujensa väristen sivujen leikkauksessa. Edelleen sanomme kärki- tai särmäpalan olevan oikeassa paikassa ja oikeassa asennossa, jos se on oikeassa paikassa, ja jos sen jokainen ruutu on oikeanvärisellä sivulla. Oheisessa kuvassa kuutio on tilassa, jossa kaikki kärki- ja särmäpalat ovat oikeilla paikoillaan, mutta etusivun kaksi kärkipalaa ja yläkerroksen kaksi särmäpalaa ovat väärissä asennoissa. Myöhemmin näemme, että tähän tilanteeseen itse asiassa päästään alkutilanteesta tietyllä siirtosarjalla.
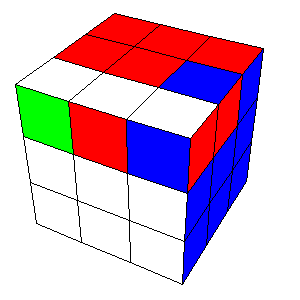
Jos perussiirtojen avulla saadaan aikaan kuution osien permutaatiot s ja t, niin suorittamalla vastaavat siirtosarjat peräkkäin (ensin t, sitten s) saadaan permutaatio st. Näin ollen mahdollisten siirtosarjojen antamat permutaatiot muodostavat permutaatioryhmän, jota kutsumme Rubikin ryhmäksi G(Rubik). Rubikin ryhmä muodostuu tässä kuution 54 ruudun joistakin permutaatioista, joten G(Rubik) on näin ajateltavissa ryhmän S54 osajoukoksi. Edelleen siirtosarjaa vastaavan permutaation s käänteispermutaatio s-1 saadaan "käännetystä siirtosarjasta" eli peruuttamalla tehdyt perussiirrot käännetyssä järjestyksessä. Esimerkiksi, jos permutaatio s saadaan siirtosarjalla "etumyota,oikeaalas,kansiplus", niin siirtosarja "kansimiinus,oikeaylos,etuvasta" antaa permutaation s-1. Koska kyse on viime kädessä funktioiden yhdistämisestä, tämä vastaa koulumatematiikasta tuttua yhdistetyn funktio käänteisfunktion lauseketta
Usein on hyödyllistä tarkastella vain sitä, miten Rubikin ryhmän permutaatiot liikuttavat kokonaisia paloja ja unohtaa näiden palojen asennot (ts. ei välitetä siitä, miten yksittäiset ruudut liikkuvat). Tällöin saamme ryhmän G(paikat), jonka voidaan ajatella olevan ryhmän S(kärjet ja särmät)=S20 osajoukko (20 paikkaa = 8 kärkeä + 12 särmää). Tällöin kuitenkin olemme hukanneet informaatiota - emme tiedä enää mitään palojen asennosta. Palojen asentoja voimme myös kuvata permutaatioryhmällä G(asennot), joka muodostuu sellaisista Rubikin ryhmän permutaatioista, jotka jättävät kaikki kärki- ja särmäpalat oikeille paikoilleen, mutta mahdollisesti vääriin asentoihin.
Ryhmä G(asennot) on selvästi Rubikin ryhmän osajoukko. Voimme todistaa, että G(asennot) on Rubikin ryhmän normaali aliryhmä. Ryhmien G(Rubik) ja G(paikat) suhde sen sijaan on hieman mutkikkaampi. Matematiikassa tähän samojen permutaatioiden eri tarkastelutapoihin liittyvä informaation menetys vastaa tekijäryhmän käsitettä. Itse asiassa meidän kolmea permutaatioryhmäämme sitoo toisiinsa relaatio
Tarkastellaan ensin yleisiä suuntaviivoja, eli sitä minkälaisia vaiheita ryhmäteoreettisessa algoritmissamme voisi olla. Lähtötilannehan on jokin Rubikin ryhmän permutaatio. Esiteltävän algoritmin ideana on jatkuvasti tehdä siirtosarjoja, joiden jälkeen kuution tilaa kuvaava permutaatio kuuluu aina pienempään ja pienempään Rubikin ryhmän aliryhmään.
Algebrallisesti (vaan ei visuaalisesti) on luontevaa yrittää ensin huolehtia siitä, että palat ovat oikeilla paikoillaan (mutta eivät välttämättä oikeissa asennoissa), eli ensin haluamme palauttaa annetun Rubikin ryhmän permutaation aliryhmän G(asennot) permutaatioksi. Toinen mahdollisuus (algoritmin etenemisen visuaalisen hahmottamisen kannalta jopa parempi) olisi keskittyä ensin esimerkiksi kärkipaloihin ja sitten särmäpaloihin.
Jaamme algoritmin karkeasti viiteen eri vaiheeseen:
Näistä ensimmäinen vaihe on helppo toteuttaa. Näemme nimittäin heti, että ryhmässä G(paikat) on ainoastaan parillisia permutaatioita. Tämä johtuu siitä, että perussiirrot vastaavat ryhmässä kahden 4-syklin tuloa (yksi 4-sykli permutoi kärkipaloja ja toinen särmäpaloja). Näin ollen kuution jokaisessa mahdollisessa tilassa kärkipalojen paikkoihin ja särmäpalojen paikkoihin on joko molempiin kohdistunut parillinen permutaatio tai molempiin pariton permutaatio sen mukaan, onko perussiirtoja tehty alkutilanteesta lähtien parillinen vai pariton määrä. Jos siis kärkipaloihin ja särmäpaloihin on kohdistunut pariton permutaatio, tekemällä minkä tahansa sivujen keskiruudut paikallaan pitävän perussiirron pääsemme haluttuun tilanteeseen.
Algoritmimme muut vaiheet perustuvat kukin yhden vakiosiirtosarjan ja sen konjugaattien käyttöön. Alkuosan teorian nojalla mikä tahansa parillinen permutaatio voidaan tuottaa 3-syklien avulla, joten on luonnollista etsiä paikkojen 3-syklejä. Nämä on alla tuotettu sopivina kommutaattoreina ryhmäteoreettissä osiossa esitellyllä tavalla. Hyvin samanhenkisten kommutaattorien avulla löydämme helposti siirtosarjat, jotka kääntävät kahta vierekkäistä särmäpalaa paikoillaan tai kahta vierekkäistä kärkipalaa - toista myötäpäivään toista vastapäivään. Myöhemmin osoitamme, että näiden siirtosarjojen avulla saamme tuotettua kaikki ryhmän G(asennot) permutaatiot. Näin tuleekin algoritmimme valmiiksi.
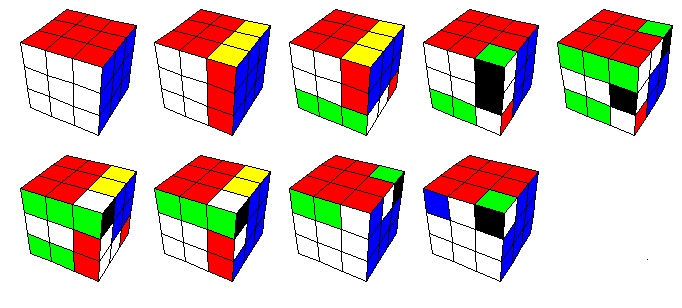
Kaikenkaikkiaan tämä siirtosarja on
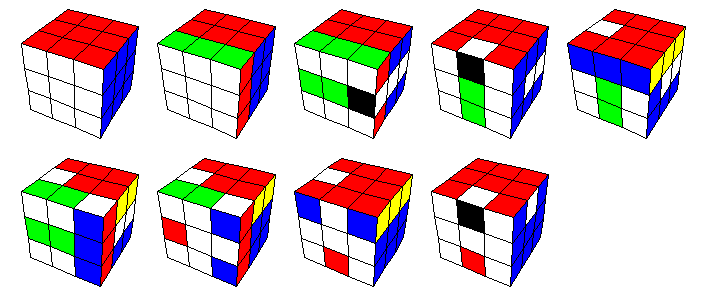
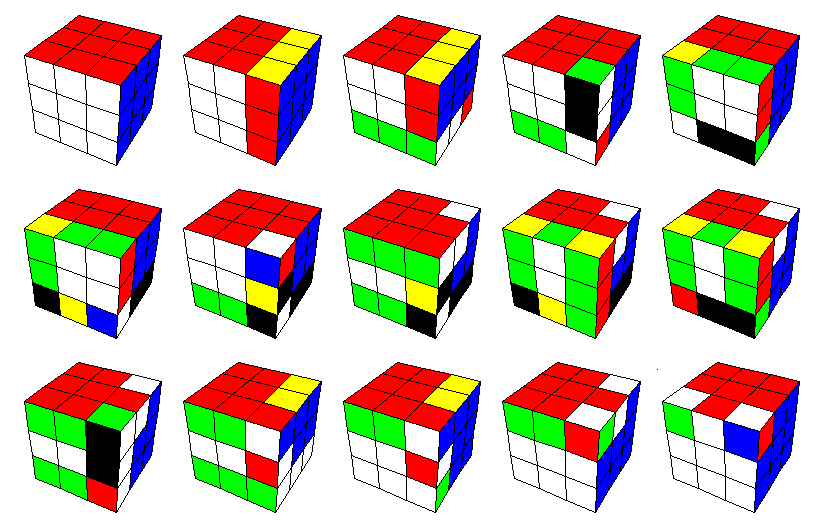
Tämäkin siirtosarja on konstruoitu kommutaattorina. Ensimmäiset kuusi siirtoa antavat permutaation t-1, joka jättää kuution ylimmän kolmanneksen koskemattomaksi lukuun ottamatta etusivun oikeanpuoleista yläkärkeä, joka on kiertynyt paikallaan 120 astettta, kaksi alinta kerrosta menivät tietenkin sekaisin. Sitten on tehty yläkerran kierto s-1. Kun seuraavaksi peruutetaan aluksi tehty siirtosarja (vastaten permutaatiota t), niin kaksi alinta kerrosta palautuvat alkutilaan ja oikeassa etuylänurkassa nyt oleva kärkipala kiertyy paikallaan 120 astetta vastakkaiseen suuntaan. Kun lopuksi kumotaan yläkerran kierto, on haluttu siirtosarja [s,t] valmis.
Tämäkin siirtosarja on kommutaattori. Se eroaa kärkipalojen kierron antavasta siirtosarjasta ainoastaan siirtosarjan t osalta. Tällä kertaa t-1 on seitsemän siirron sarja, joka jättää yläkerran entiselleen oikeanpuoleista särmäpalaa lukuun ottamatta ja kääntää tuon särmäpalan paikallaan. Kuten aiemmin, kuution yläkerran kierron s ja siirtosarjan t kommuttaatori [s,t] on haluttu siirtosarja.
Vaihe 2 - kärkipalat paikoilleen
Vaiheen 1 jälkeen tiedämme, että kärkipalojen paikkoihin on kohdistunut parillinen permutaatio. Tämä permutaatio saadaan 3-syklejä kombinoimalla. Yksi systemaattinen tapa valita seuraavaksi tehtävä 3-sykli on seuraava: Olkoon A jokin väärässä paikassa oleva kärkipala. Tällöin palan A oikealla paikalla on kärkipala B, joka ei tietenkään myöskään ole oikealla paikallaan. Jos A ja B olisivat ainoat väärillä paikoilla olevat kärkipalat, niin kärkipaloihin olisi kohdistunut 2-sykli (AB), mikä on pariton permutaatio. Näin ollen on olemassa kärkipala C (eri kuin A ja B), joka on väärässä paikassa. Jos teemme 3-syklin (ABC), niin sen seurauksena kärkipala A siirtyy oikealle paikalleen, eikä yhtään oikealla paikalla olevaa kärkipalaa siirry väärälle paikalle. Näin ollen oikealla paikalla olevien kärkipalojen lukumäärä kasvaa 3-syklin (ABC) seurauksena. Toistamalla prosessia riittävän monta kertaa, saame lopulta kaikki kärjet oikeille paikoilleen.
Mutta mutta? Pystymmekö välttämättä toteuttamaan minkä tahansa kärkipalojen 3-syklin. Aiemmin kuvattu esimerkki toimii siinä tapauksessa, että 3-sykliin osallistuvat kärkipalat ovat kaikki samalla sivulla (helposti näet, että tällöin kuutiota kääntelemällä saat halutut 3 kärkipalaa etusivun kuvattuihin kärkiin). Muut kärkien 3-syklit saadaan kuitenkin kuvattua 3-sykliä konjugoimalla: Jos esimerkiksi haluamme tehdä 3-syklin, johon osallistuvat etusivun vasen yläkärki, etusivun oikea alakärki ja takasivun oikea yläkärki, niin ennen kuvattua siirtosarjaa [s,t] teemmekin siirtosarjan g="pohjamiinus,oikeaalas", jolloin siirrossa "pohjamiinus" etusivun oikea alakärki siirtyy etusivun vasemmaksi alakärjeksi, ja siirrossa "oikeaalas" takasivun oikea yläkärki siirtyy etusivun oikeaksi yläkärjeksi. 3-syklin [s,t] jälkeen sitten lopuksi peruutamme tehdyt siirrot sarjalla g-1. Kaiken kaikkiaan tämä 3-sykli saadaan siis permutaationa g-1 [s,t] g.
Lisäksi on mahdollista, että 3-sykli pyörii "väärään suuntaan", eli teemmekin syklin (ACB) syklin (ABC) sijasta. Tästä tosin selviämme helposti, sillä (ABC)=(ACB)-1, eli käännämme vain siirtosarjan aiemmin kuvatulla tavalla. Jos olet vahingossa tehnyt väärään suuntaan pyörivän 3-syklin, niin älä masennu. Toistamalla sama siirtosarja saat oikeaan suuntaan pyörivän 3-syklin, sillä (ABC)(ABC)=(ACB).
Vaihe 3 - särmäpalat paikoilleen
Tästä vaiheesta selvitään nyt samoin kuin vaiheesta 2. Tekemällä aiemmin kuvatun särmäpalojen 3-syklin sopivia konjugaatteja riittävä määrä, särmäpalat menevät lopulta oikeille paikoilleen.
Vaihe 4 - kärkipalat oikeihin asentoihinsa
Tässä vaiheessa voimme olettaa, että kaikki kärkipalat jo ovat oikeilla paikoillaan. Ne saadaan oikeihin asentoihin kombinoimalla kuvattua siirtosarjaa ja sen sopivia konjugaatteja. Tässä ei välttämättä tarvitse turvautua konjugaatteihin, jos on halukas toistamaan ko. siirtosarjaa "tarpeettomasti". Yksi systemaattinen tapa on edetä kärki kerrallaan järjestyksessä "oikea etuylä, oikea takaylä, vasen takaylä, vasen etuylä, vasen etuala, oikea etuala, oikea taka-ala, vasen taka-ala". Tässä jonossa mitkä tahansa kaksi peräkkäistä kärkeä ovat samalla särmällä, joten katsomalla kuutiota sellaisesta suunnasta, jossa kyseinen särmä tulee etusivun yläreunaksi, voimme käyttää tarvittaessa kuvattua siirtosarjaa (tai sen käänteistä sarjaa) siihen, että jonossa aiemmin esiintyvä kärki kääntyy oikeaan asentoonsa. Tällöin emme välitä siitä, mitä jonossa seuraavana olevalle "apukärjelle" tapahtuu.
Mutta mutta? Miten käy jonon viimeisen kärjen? Sillehän emme enää voi tarjoa toista "apukärkeä" kaveriksi. Osoittautuu, että se ei ole tarpeen! Jonon kaksi viimeistä kärkeä nimittäin kääntyvät yhtä aikaa oikeihin asentoihinsa. Nimittäin tilanteessa, jossa kaikki kärkipalat ovat oikeilla paikoillaan voimme määrätä "kokonaiskiertymän" laskemalla yhteen kunkin kärkipalan kiertymät:
Vaihe 5 - särmäpalat oikeihin asentoihinsa
Kuvattu siirtosarja esittää, miten kaksi vierekkäistä särmäpalaa voidaan kääntää. On selvää, että tätä siirtosarjaa konjugoimalla saamme käännettyä mitkä tahansa kaksi särmäpalaa. Jos voisimme olla varmoja, että kääntyneitä särmäpaloja on aina parillinen määrä, niin tämä riittääkin - käännämme särmäpalat pareittain. Itse asiassa näin onkin. Sen näkemiseksi tarkastelkaamme sitä, miten Rubikin ryhmä operoi 24 särmäpalasivun (12 särmäpalaa, 2 sivua kullakin) joukossa. Näemme, että perussiirrot vastaavat tässä aina kahden 4-syklin tuloa. Tämä on parillinen permutaatio, joten 24 särmäpalasivuun kohdistuu tulosäännön nojalla aina parillinen permutaatio. Jos olisi mahdollista kääntää yksi (tai mikä tahansa pariton määrä) särmäpala paikallaan, syntyisi särmäpalasivujen joukkoon pariton permutaatio (nimittäin 2-sykli). Osoitimme juuri, että Rubikin ryhmässä ei tällaisia permutaatioita ole.
Yhteenveto, kombinaatioiden lukumäärä
Olemme nähneet vaiheissa 4 ja 5, että ryhmässä G(asennot) on alkioita 21137. Kullakin 12 särmäpalallahan on 2 mahdollista asentoa, mutta viimeisen asento määräytyy muiden asennoista siten, että väärinpäin olevia on parillinen määrä. Edelleen kullakin 8 kärkipalalla on 3 mahdollista asentoa, mutta viimeisen asento määräytyy siitä, että kokonaiskiertymä on 360 asteen kokonaislukumonikerta.
Vastaavasti näimme, että ryhmällä G(paikat) on aliryhmä H, joka muodostuu niistä permutaatioista, jotka operoivat sekä kärkipaloihin että särmäpaloihin parillisella permutaatiolla. Itse asiassa aliryhmässä H on tasan puolet ryhmän G(paikat) alkioista, sillä G(paikat) on erillisten osajoukkojensa H ja "oikeaalas"H unioni. Todistus. Vaiheissa 2 ja 3 näimme, että ryhmässä H ovat kaikki kärkipalojen parillisten permutaatioiden ja särmäpalojen parillisten permutaatioiden kombinaatiot. Näin ollen ryhmän G(paikat) alkioiden lukumäärä on 2 (8!/2) (12!/2). Ryhmäteoriaa tuntevat huomaavat varmaankin, että H on itse asiassa isomorfinen ryhmien A8 ja A12 suoran tulon kanssa.
Kaiken kaikkiaan siis Rubikin ryhmän alkioiden lukumääräksi saadaan
Rubikin ryhmän kompositiotekijöinä esiintyvät 2 alkion syklinen ryhmä (12 kertaa), 3 alkion syklinen ryhmä (7 kertaa) sekä alternoivat ryhmät A8 ja A12 (kumpikin kerran). Ryhmäteorian alkeita tuntevat huomaavat nyt heti, että Rubikin ryhmä ei ole ryhmäteorian mielessä ratkeava. Onneksi pulmapeli kuitenkin on ratkeava, kuten juuri näimme.