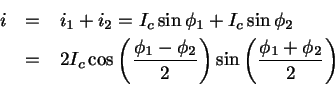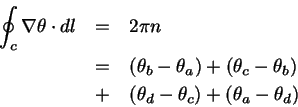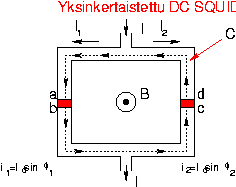
1. ja 3. termi ovat yli J-liitosten, joten
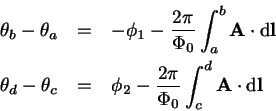
2. ja 4. termi ovat SC:ssä ja saadaan
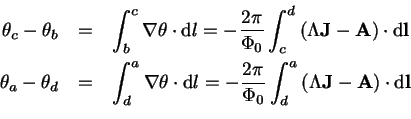
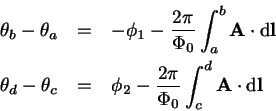
2. ja 4. termi ovat SC:ssä ja saadaan
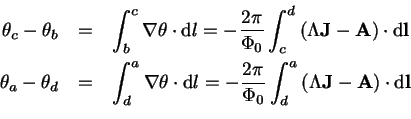
Sijoittamalla saadaan ( on C josta on poistettu J-liitokset)
on C josta on poistettu J-liitokset)
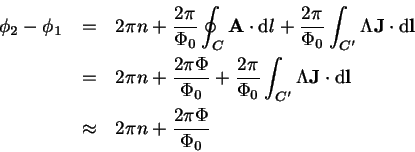
Joten virta on
on
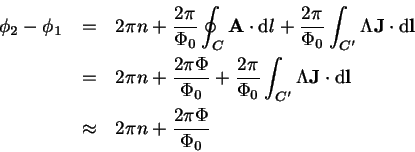
Joten virta
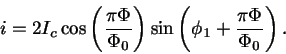 |
Jos renkaan induktanssi on 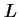 saadaan
saadaan
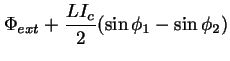 |
|||
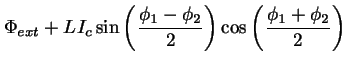 |
|||
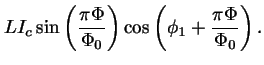 |
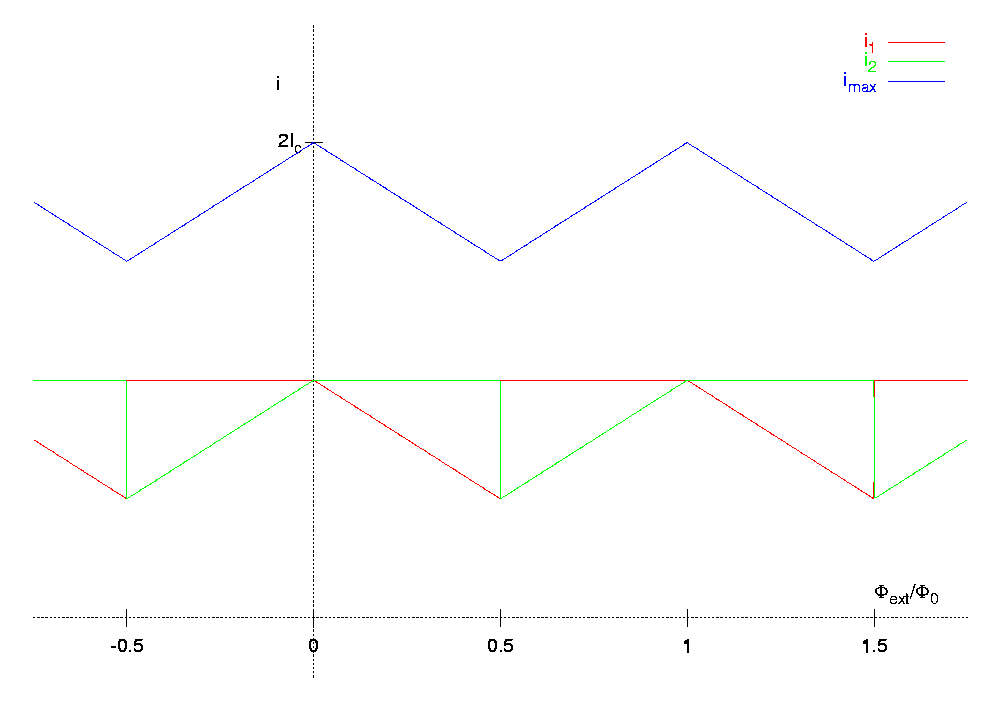
Erikoistapaus

Lasketaan
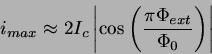
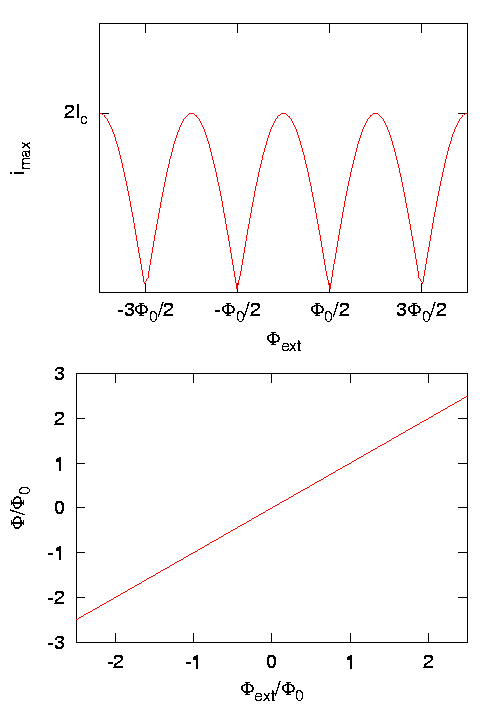
Yleinen tapaus
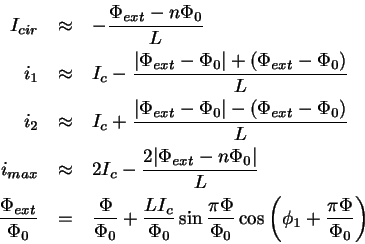
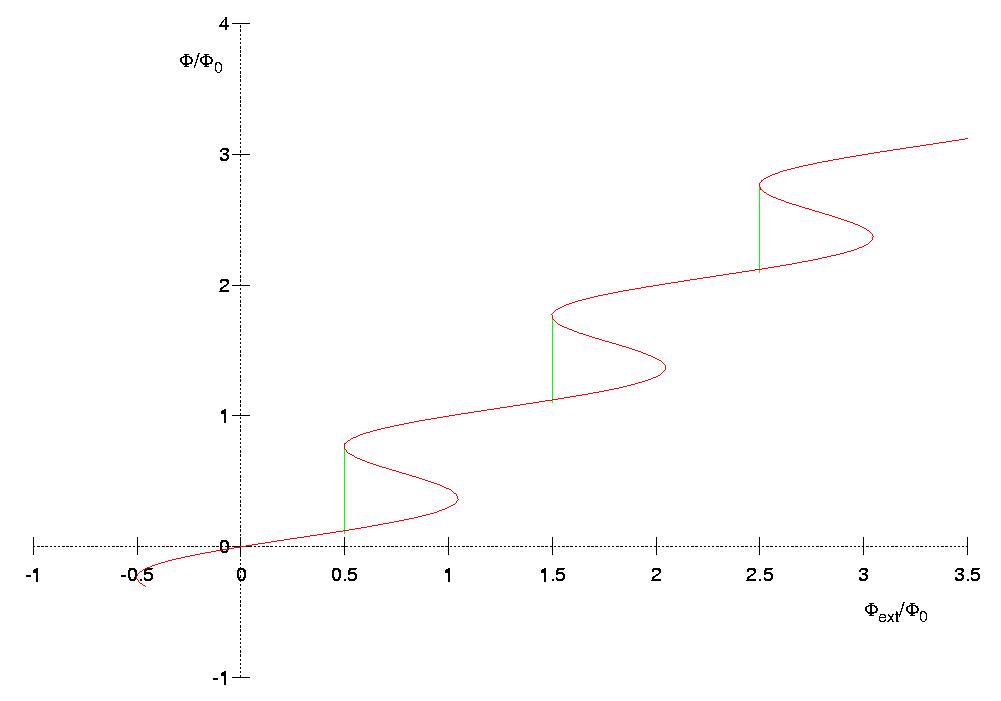
Ajettaessa virta 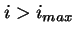 SQUIDin yli muodostuu jännite, joka DC
komponentti on
SQUIDin yli muodostuu jännite, joka DC
komponentti on
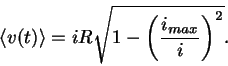
Koska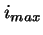 on jaksollinen ulkoisen kentän mukana, voidaan
jännitteen ilmestymistä käyttää ulkoisen magneettikentän mittarina.
on jaksollinen ulkoisen kentän mukana, voidaan
jännitteen ilmestymistä käyttää ulkoisen magneettikentän mittarina.
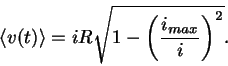
Koska
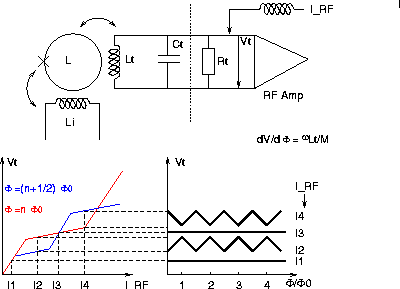
RF SQUID
Next: RSFQ Up: Elektroniikan sovellukset Previous: Josephsonin liitokset Sisältö Petriina Paturi 2003-10-17