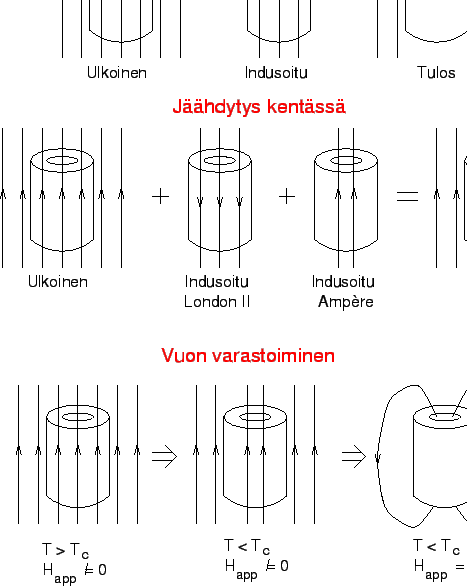
Ajatellaan suprajohtavaa onttoa sylinteriä SLIDE 23. Jos kenttä pistetään päälle kun sylinteri on jo suprajohtavassa tilassa, suprajohde indusoi suojausvirran ulkoreunalleen ja vuo ei pääse tunkeutumaan reikään ja tulos on yläkuvan mukainen. Jos taas kenttä on jo päällä sylinteriä jäähdytettäessä, indusoituu virta sekä ulko- että sisäreunalle ja tulos on keskimmäisen kuvan mukainen. Jos nyt poistetaan ulkoinen kenttä, jää sylinterin läpäisevä vuo ennalleen ja näin vuo on pysyvästi jumiintunut. Koska tällainen varastoitunut vuo voidaan mitata hyvin tarkasti sitä tuhoamatta, on tehty kokeita, joissa vuo on varastoitu vuosiksi ilman, että siinä on huomattu mitään vähenemistä. Näillä kokeilla on siis voitu todeta tarkemmin kuin millään resistanssin mittauksella, että suprajohteen DC resistanssi on nolla.
Edellä huomasimme, että suprajohderenkaan sisälle voidaan varastoida magneettivuo. Voiko tämä vuo olla mielivaltaisen pieni ? Vastaus on ei, mutta sen ymmärtämiseksi joudumme käsittelemään nopeasti suprajohtavuuden kvanttimekaanisia ominaisuuksia. (Joudumme perehtymään tähän nyt, jotta myöhemmin ymmärtäisimme Josephson-liitoksia käyttäviä sovelluksia). Tarkastelemme Ginzburg-Landau teoriaa SLIDE 24.
| (31) |
 |
 |
(34) | |
 |
(35) | ||
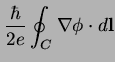 |
(36) | ||
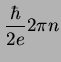 |
(37) | ||
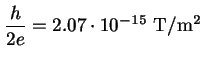 |
(38) |
Vuon kvantittumista SLIDE 25,SLIDE 26 voidaan tutkia
kokeellisesti, ja näin varmistua teorian paikkansa
pitävyydestä. SLIDE 27:ssa nähdään tulokset Deaverin ja Fairbankin
1961 tekemästä kokeesta, jossa jäähdytettiin suprajohtavaa onttoa
sylinteriä eri ulkoisissa kentissä ja mitattiin sen sisälle jumiutunut
vuo. Kuten kuvasta huomataan, vuo kasvoi porrasmaisesti ja vielä
siten, että portaan korkeus vastasi varauksenkuljettajan varausta
![]() , mikä vahvisti edelleen BCS-teorian mukaisen oletuksen
elektronipareista.
, mikä vahvisti edelleen BCS-teorian mukaisen oletuksen
elektronipareista.
Vuon kvantittuminen jakaa suprajohdemateriaalit kahteen
luokkaan. Tyypin I on energeettisesti helpompaa minimoida
suprajohtavan ja normaalin materiaalin rajapinta, kun taas tyypille II
on helpompaa maksimoida ko. rajapinta. Tästä seuraa, että tyypillä II
esiintyy ns. sekatila ensimmäisen kriittisen kentän yläpuolella, jossa
sen sisällä on normaaleja alueita, joita läpäisee yksi
vuokvantti. Näitä kutsutaan vortekseiksi. Tämä ero aiheuttaa
luonnollisesti eron myös ![]() -diagrammiin SLIDE 28.
-diagrammiin SLIDE 28.