Edellisessä kohdassa näimme, miten hyvää sähkönjohdetta approksimoitiin kuvittelemalla se täydelliseksi, jossa sähkökenttään ei varastoidu lainkaan energiaa. Suprajohteita käsiteltäessä haluaisimme tietenkin mallin, joka kuvaa oikeasti täydellistä johdetta, mutta SLIDE 13.
Tarvitsemme siis uuden tavan lähestyä asiaa. Käytämme Druden mallia
kiinteille aineille. Siinä oletetaan, että elektronit ovat pieniä
kiinteitä palloja, jotka liikkuvat paikallisen sähkökentän
vaikutuksesta. Lisäksi elektronien keskinäiset vuorovaikutukset
jätetään tarkoituksella pois. Kun kirjoitetaan tällaisten otusten
liikeyhtälö saadaan SLIDE 14, jossa ![]() on siroamisaika,
eli aika joka kuluu kahden törmäyksen välillä. Tässä
on siroamisaika,
eli aika joka kuluu kahden törmäyksen välillä. Tässä ![]() on
puhtaasti kokeellinen parametri, jonka arvo saadaan epäsuorasti kokeista.
Esimerkin omaisesti yhtälöstä (27) voidaan laskea siroamisaika
kuparille, jonka johtavuus
huoneenlämpötilassa
on
puhtaasti kokeellinen parametri, jonka arvo saadaan epäsuorasti kokeista.
Esimerkin omaisesti yhtälöstä (27) voidaan laskea siroamisaika
kuparille, jonka johtavuus
huoneenlämpötilassa
![]() S/m ja varauksen kuljettajien
tiheys suurinpiirtein
S/m ja varauksen kuljettajien
tiheys suurinpiirtein
![]() kpl/m
kpl/m![]() . Tästä saadaan
siroamisajalle
. Tästä saadaan
siroamisajalle
![]() s ja voidaan
todeta, että
s ja voidaan
todeta, että
![]() niinkin korkeilla taajuuksilla
kuin 1 THz. Eli kuparin johtavuus on lähes riippumaton taajuudesta.
niinkin korkeilla taajuuksilla
kuin 1 THz. Eli kuparin johtavuus on lähes riippumaton taajuudesta.
| (20) |
| (21) | |||
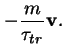 |
(22) |
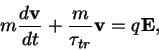 |
(23) |
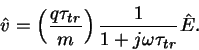 |
(24) |
| (26) |
Soveltamalla edellä laskettua taajuusriippuvaista Ohmin lakia
täydelliseen johteeseen, tehdään muutos
![]() . Systeemiä voidaan verrata RL-piiriin, jossa vastus poistetaan
ja jäljelle jää vain ideaalinen kela. Ratkaistaksemme ongelmia
täydellisessä johteessa oikein, meidän täytyy käyttää SLIDE 15:n
Ohmin lakia ja johtaa näin uudet MQS yhtälöt. Samoin kuin aiemminkin
saadaan SLIDE 17. Kun näitä sovelletaan äärellisen paksuiseen
äärettömään levyyn (SLIDE 18), joka on ac-magneettikentässä, saadaan
SLIDE 19 mukainen magneettikentän jakauma.
. Systeemiä voidaan verrata RL-piiriin, jossa vastus poistetaan
ja jäljelle jää vain ideaalinen kela. Ratkaistaksemme ongelmia
täydellisessä johteessa oikein, meidän täytyy käyttää SLIDE 15:n
Ohmin lakia ja johtaa näin uudet MQS yhtälöt. Samoin kuin aiemminkin
saadaan SLIDE 17. Kun näitä sovelletaan äärellisen paksuiseen
äärettömään levyyn (SLIDE 18), joka on ac-magneettikentässä, saadaan
SLIDE 19 mukainen magneettikentän jakauma.
Valitettavasti suprajohdetta ei voida kuvata täydellisenä johteena. Tämä huomataan seuraavasta ajatuskokeesta (SLIDE 20). Jos pallo, joka on tehty täydellisestä johteesta, jäähdytetään ilman kenttää kriittisen lämpötilan alapuolella, ja sen jälkeen kytketään magneettikenttä päälle, se sulkee magneettikentän sisältään. Näin toimii myös suprajohde. Ero tulee kun pallo jäähdytetään kentässä: täydellinen johde säilyttää kentän sisällään ja suprajohde sulkee sen ulos SLIDE 21. Tämä on Meissnerin ilmiö.